以下,これを示す。 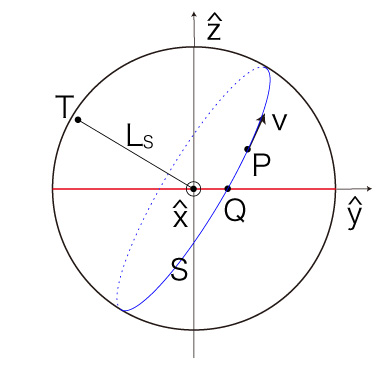
\( L_S \) が球面と交わる2点のうち,
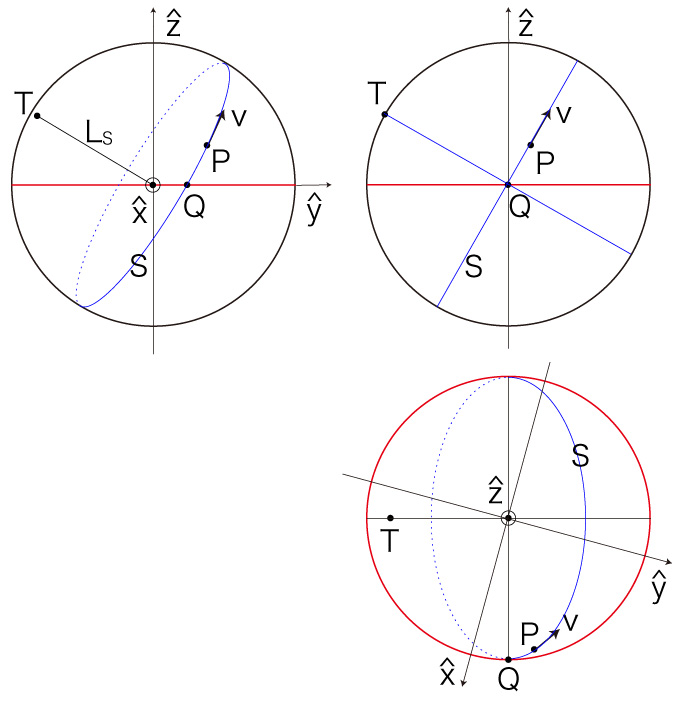
先ず,条件 \[ | \vec{OP} | = R \\ \ \\ | \vec{OT} | = R \\ \vec{OT} \cdot \vec{OP} = 0 \\ \ \\ | \vec{OQ} | = R \\ \vec{OT} \cdot \vec{OQ} = 0 \\ \] を座標に表現すると \[ {P_{\hat{x}}}^2 + {P_{\hat{y}}}^2 + {P_{\hat{z}}}^2 = R^2 \\ \ \\ {T_{\hat{x}}}^2 + {T_{\hat{y}}}^2 + {T_{\hat{z}}}^2 = R^2 \\ T_{\hat{x}}\ P_{\hat{x}} + T_{\hat{y}}\ P_{\hat{y}} + T_{\hat{z}}\ P_{\hat{z}} = 0 \\ \ \\ {Q_{\hat{x}}}^2 + {Q_{\hat{y}}}^2 = R^2 \\ T_{\hat{x}}\ Q_{\hat{x}} + T_{\hat{y}}\ Q_{\hat{y}} = 0 \\ \] 残る条件は,\( \vec{OT},\ \vec{OP},\ {\bf{ v }} \) の間の「右ネジ」の条件であり,これは \[ \frac{ \vec{OT} \times \vec{OP} }{ | \vec{OT} \times \vec{OP} | } = \frac{ {\bf{ v }} }{ | {\bf{ v }} | } \\ \] そしてこれを座標に表現すると \[ \vec{OT} \times \vec{OP} = ( T_{\hat{x}},\ T_{\hat{y}},\ T_{\hat{z}} ) \times (P_{\hat{x}},\ P_{\hat{y}},\ P_{\hat{z}} )\\ = (T_{\hat{y}}\ P_{\hat{z}} - T_{\hat{z}}\ P_{\hat{y}},\ T_{\hat{z}}\ P_{\hat{x}} - T_{\hat{x}}\ P_{\hat{z}},\ T_{\hat{x}}\ P_{\hat{y}} - T_{\hat{y}}\ P_{\hat{x}} ) \\ \ \\ | \vec{OT} \times \vec{OP} | = | \vec{OT} |\ | \vec{OP} |\ sin( \pi / 2 ) = R^2 \\ \ \\ \frac{ {\bf{ v }} }{ v } = \bigl(\ \frac{ v_{\hat{x}} }{ v },\ \frac{ v_{\hat{y}} }{ v },\ \frac{ v_{\hat{z}} }{ v }\ \bigr) \\ \] ここで \[ v = | {\bf{ v }} | \\ \] よって, \[ T_{\hat{y}}\ P_{\hat{z}} - T_{\hat{z}}\ P_{\hat{y}} = \frac{ R^2 }{ v }\ v_{\hat{x}} \\ T_{\hat{z}}\ P_{\hat{x}} - T_{\hat{x}}\ P_{\hat{z}} = \frac{ R^2 }{ v }\ v_{\hat{y}} \\ T_{\hat{x}}\ P_{\hat{y}} - T_{\hat{y}}\ P_{\hat{x}} = \frac{ R^2 }{ v }\ v_{\hat{z}} \\ \] ここで,\( P_z \ne 0 \) と \( P_z = 0 \) の2つの場合にわける。 先の3式は,一つの式が残り2つの式の含意になり,実質2式である。 最初の2つの式から, \[ T_{\hat{y}}\ P_{\hat{z}} - T_{\hat{z}}\ P_{\hat{y}} = \frac{ R^2 }{ v }\ v_{\hat{x}} \\ \quad \Longrightarrow T_{\hat{y}} = \frac{1}{P_{\hat{z}}}\ \bigl( T_{\hat{z}}\ P_{\hat{y}} + \frac{ R^2 }{ v }\ v_{\hat{x}} \bigr) = \frac{ P_{\hat{y}} }{ P_{\hat{z}} }\ T_{\hat{z}} + \frac{ R^2\ v_{\hat{x}} }{ v\ P_{\hat{z}} } \\ \ \\ T_{\hat{z}}\ P_{\hat{x}} - T_{\hat{x}}\ P_{\hat{z}} = \frac{ R^2 }{ v }\ v_{\hat{y}} \\ \quad \Longrightarrow T_{\hat{x}} = \frac{1}{P_{\hat{z}}}\ \bigl( T_{\hat{z}}\ P_{\hat{x}} - \frac{ R^2 }{ v }\ v_{\hat{y}} \bigr) = \frac{ P_{\hat{x}} }{ P_{\hat{z}} }\ T_{\hat{z}} - \frac{ R^2\ v_{\hat{y}} }{ v\ P_{\hat{z}} } \\ \] これを \[ T_{\hat{x}}\ P_{\hat{x}} + T_{\hat{y}}\ P_{\hat{y}} + T_{\hat{z}}\ P_{\hat{z}} = 0 \\ \] に代入: \[ \bigl( \frac{ P_{\hat{x}} }{ P_{\hat{z}} }\ T_{\hat{z}} - \frac{ R^2\ v_{\hat{y}} }{ v\ P_{\hat{z}} } \bigr)\ P_{\hat{x}} + \bigl( \frac{ P_{\hat{y}} }{ P_{\hat{z}} }\ T_{\hat{z}} + \frac{ R^2\ v_{\hat{x}} }{ v\ P_{\hat{z}} })\ P_{\hat{y}} + T_{\hat{z}}\ P_{\hat{z}} = 0 \\ \ \\ \ \\ \bigl( \frac{ P_{\hat{x}}^2 }{ P_{\hat{z}} } + \frac{ P_{\hat{y}}^2 }{ P_{\hat{z}} } + P_{\hat{z}} \bigr)\ T_{\hat{z}} - \frac{ R^2\ P_{\hat{x}}\ v_{\hat{y}} }{ v\ P_{\hat{z}} } + \frac{ R^2\ P_{\hat{y}}\ v_{\hat{x}} }{ v\ P_{\hat{z}} } =0 \\ \ \\ \ \\ \frac{ P_{\hat{x}}^2 + P_{\hat{y}}^2 + P_{\hat{z}}^2 }{ P_{\hat{z}} }\ T_{\hat{z}} - R^2\ \frac{ P_{\hat{x}}\ v_{\hat{y}} - P_{\hat{y}}\ v_{\hat{x}} }{ v\ P_{\hat{z}} } =0 \\ \ \\ \ \\ T_{\hat{z}} = \frac{ P_{\hat{x}}\ v_{\hat{y}} - P_{\hat{y}}\ v_{\hat{x}} }{ v } \] よって, \[ \begin{align} T_{\hat{x}} &= \frac{ P_{\hat{x}} }{ P_{\hat{z}} }\ T_{\hat{z}} - \frac{ R^2\ v_{\hat{y}} }{ v\ P_{\hat{z}} } \\ &= \frac{ P_{\hat{x}} }{ P_{\hat{z}} }\ \frac{ P_{\hat{x}}\ v_{\hat{y}} - P_{\hat{y}}\ v_{\hat{x}} }{v} - \frac{ R^2\ v_{\hat{y}} }{ v\ P_{\hat{z}} } \\ &= \frac{ P_{\hat{x}}^2\ v_{\hat{y}} - P_{\hat{x}}\ P_{\hat{y}}\ v_{\hat{x}} - R^2\ v_{\hat{y}} }{ v\ P_{\hat{z}} } \\ \ \\ T_{\hat{y}} &= \frac{ P_{\hat{y}} }{ P_{\hat{z}} }\ T_{\hat{z}} + \frac{ R^2\ v_{\hat{x}} }{ v\ P_{\hat{z}} } \\ &= \frac{ P_{\hat{y}} }{ P_{\hat{z}} }\ \frac{ P_{\hat{x}}\ v_{\hat{y}} - P_{\hat{y}}\ v_{\hat{x}} }{v} + \frac{ R^2\ v_{\hat{x}} }{ v\ P_{\hat{z}} } \\ &= \frac{ P_{\hat{x}}\ P_{\hat{y}}\ v_{\hat{y}} - P_{\hat{y}}^2\ v_{\hat{x}} + R^2\ v_{\hat{x}} }{ v\ P_{\hat{z}} } \\ \end{align} \] ここで,つぎのように措く: \[ T_{\hat{x}} = \frac{ A }{ v\ P_{\hat{z}} } \\ T_{\hat{y}} = \frac{ B }{ v\ P_{\hat{z}} } \\ \ \\ \quad A = P_{\hat{x}}^2\ v_{\hat{y}} - P_{\hat{x}}\ P_{\hat{y}}\ v_{\hat{x}} - R^2\ v_{\hat{y}} \\ \quad B = P_{\hat{x}}\ P_{\hat{y}}\ v_{\hat{y}} - P_{\hat{y}}^2\ v_{\hat{x}} + R^2\ v_{\hat{x}} \\ \] これを \[ T_{\hat{x}}\ Q_{\hat{x}} + T_{\hat{y}}\ Q_{\hat{y}} = 0 \] に代入: \[ Q_{\hat{x}}\ \frac{ A }{ v\ P_{\hat{z}} } \ \ + Q_{\hat{y}}\ \frac{ B }{ v\ P_{\hat{z}} }\ = 0 \\ \ \\ \quad \Longrightarrow \ A\ Q_{\hat{x}} + B\ Q_{\hat{y}} = 0 \\ \] そして \( A\ Q_{\hat{x}} + B\ Q_{\hat{y}} = 0 \) を \[ {Q_{\hat{x}}}^2 + {Q_{\hat{y}}}^2 = R^2 \] に代入: \[ ( R^2 - Q_{\hat{x}}^2 ) = Q_{\hat{y}}^2 \\ \ \\ B^2\ ( R^2 - Q_{\hat{x}}^2 ) = B^2\ Q_{\hat{y}}^2 = A^2\ Q_{\hat{x}}^2 \\ \ \\ B^2\ R^2 = ( A^2 + B^2)\ Q_{\hat{x}}^2 \\ \ \\ \ \\ ( R^2 - Q_{\hat{y}}^2 ) = Q_{\hat{x}}^2 \\ \ \\ A^2\ ( R^2 - Q_{\hat{y}}^2 ) = A^2\ Q_{\hat{x}}^2 = B^2\ Q_{\hat{y}}^2 \\ \ \\ A^2\ R^2 = ( A^2 + B^2 )\ Q_{\hat{y}}^2 \\ \] ここで,
よって,
ここで,つぎの関係がある:
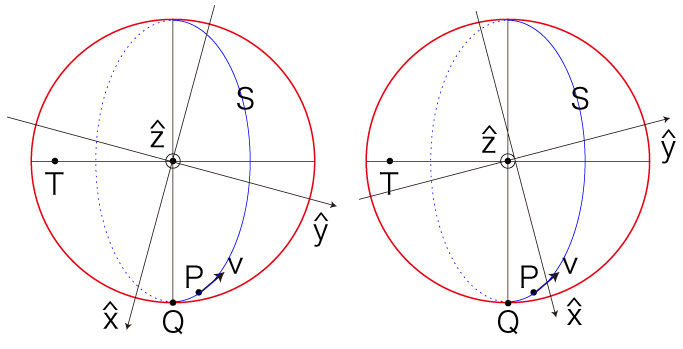
そして
即ち,
\( P_z > 0 \) のとき,
|
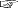 計算
計算