点 \( P = ( P'_x,\ P'_y,\ P'_z ) \) において速度が \( {\bf{v}} = ( v_x,\ v_y,\ v_z ) \) の移動は,\( \Delta t \) 後の位置 \( (P'_x,\ P'_y,\ P'_z) \) がつぎのようになる:
\[
P'_x = P_x - v_x\ cos\bigl( sin^{-1}\bigl( \frac{P_z}{R}\ \bigr) \bigr)\ \Delta t \\
P'_y = P_y + v_y\ cos\bigl( sin^{-1}\bigl( \frac{P_y}{R}\ \bigr) \bigr)\ \Delta t \\
P'_z = P_z + v_z\ cos\bigl( sin^{-1}\bigl( \frac{P_z}{R}\ \bigr) \bigr)\ \Delta t \\
\]
また,\( \Delta t \) 後の速度 \( {\bf{v}'} = ( v'_x,\ v'_y,\ v'_z ) \) は,\( P,\ {\bf{v}} \) における加速度を \( ( a_x,\ a_y,\ a_z ) \) で表すとき,つぎのようになる:
\[
v'_x = v_x + a_x\ \Delta t \\
v'_y = v_y + a_y\ \Delta t \\
v'_z = v_z + a_z\ \Delta t \\
\]
ここで加速度 \( ( a_x,\ a_y,\ a_z ) \) は,つぎのとおり:
(1) \( \bf{v} \) が赤道に乗る場合
\[
a_x = \frac{v^2}{R} + 2\ v\ \Omega + R \Omega^2 \\
a_y = 0 \\
a_z = 0 \\
\]
(2) \( \bf{v} \) が経線に乗る場合
\[
a_x = \frac{v^2 }{R^2}\ P_x + \Omega^2 \ P_x \\
a_y = 2\ \frac{ v\ \Omega }{ R }\ P_z \\
a_z = \frac{v^2}{R^2}\ P_z \\
\]
(3) それ以外
\[
a_x = \frac{v^2}{R^2}\ P_x
+ 2\ \frac{ v\ \Omega }{R}\ \frac{ P_x\ P_y }{ \sqrt{ R^2 - P_x^2 } }\ + \Omega^2\ P_x \\
a_y = \frac{v^2}{R^2}\ P_y + 2\ \frac{ v\ \Omega }{R}\ \sqrt{ R^2 - P_x^2 } + \Omega^2 \ P_y \\
a_z = \frac{v^2}{R^2}\ P_z \\
\]
さて,これを見て,「このステップを連ねることで,物体の移動を追跡できる」と思うかも知れない。
即ち,つぎの区分求積によって:
\[
P_x( 0 ) = P0_x \\
P_y( 0 ) = P0_y \\
P_z( 0 ) = P0_z \\
\ \\
v_x( 0 ) = v0_x \\
v_y( 0 ) = v0_y \\
v_z( 0 ) = v0_z \\
\ \\ \ \\
P_x( t + \Delta t ) = P_x( t ) - v_x( t )\ cos\bigl( sin^{-1}\bigl( \frac{P_z( t )}{R}\ \bigr) \bigr)\ \Delta t \\
P_y( t + \Delta t ) = P_y( t ) + v_y( t )\ cos\bigl( sin^{-1}\bigl( \frac{P_y( t )}{R}\ \bigr) \bigr)\ \Delta t \\
P_z( t + \Delta t ) = P_z( t ) + v_z( t )\ cos\bigl( sin^{-1}\bigl( \frac{P_z( t )}{R}\ \bigr) \bigr)\ \Delta t \\
\ \\
v_x( t + \Delta t ) = v_x( t ) + a_x(t)\ \Delta t \\
v_y( t + \Delta t ) = v_y( t ) + a_y(t)\ \Delta t \\
v_z( t + \Delta t ) = v_z( t ) + a_z(t)\ \Delta t \\
\]
しかし,こうはならない。
\( P,\ \bf{v} \) における加速度の式は,\( (P, \bf{v} ) \)-座標の式だからである。
<位置 \( P( t + \Delta t ) \) と速度 \( {\bf{v}}( t + \Delta t ) \) に対しこれの \( \Delta t' \) 後── \( P( ( t + \Delta t ) + \Delta t' ) \) と \( {\bf{v}}( ( t + \Delta t ) + \Delta t' ) \) ──を求めるためには,\( (P( t + \Delta t ), \bf{v}( t + \Delta t ) ) \)-座標を設定しなければならない。
移動方程式には座標変換式が含まれる,というわけである。
|
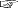 自転球体上の移動物体の, \( \Delta t \) 後の位置
自転球体上の移動物体の, \( \Delta t \) 後の位置