\( \Delta t \) 後の位置 \( P' = ( P'_x,\ P'_y,\ P'_z ) \) を,既に求めた。
ここではこれに続いて,\( \Delta t \) 後の速度 \( {\bf{v}}' = ( v'_x,\ v'_y,\ v'_z ) \) を求める。
速度
\[
{\bf{v}} = ( v_x,\ v_y,\ v_z )
\]
は,加速度
\[
{\bf{a}} = ( a_x,\ a_y,\ a_z )
\]
により,\( \Delta t \) 後につぎの速度に変わる:
\[
{\bf{v}}' = ( v'_x,\ v'_y,\ v'_z ) \\
\ \\
v'_x = v_x + a_x\ \Delta t \\
v'_y = v_y + a_y\ \Delta t \\
v'_z = v_z + a_z\ \Delta t \\
\]
これは,そっくり移動速度とはならない。
\( \Delta t \) 後の位置 \( P' = ( P'_x,\ P'_y,\ P'_z ) \) の接平面にこれを投影した \( {\bf{v}}_1 = ( {v_1}_x,\ {v_1}_y,\ {v_1}_z ) \) が,移動の実効速度になる。
この投影は,一般につぎのように計算する:
つぎの場合を考える:
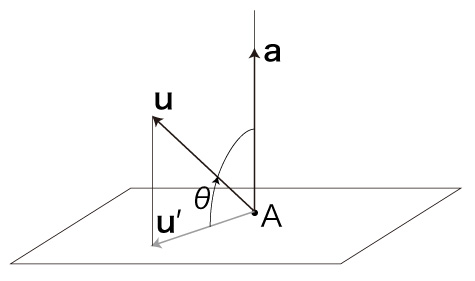
ここで,\( \bf{a} \) は,平面の法線ベクトル (単位ベクトル)。
\( \bf{u}' \) は,\( \bf{u} \) の平面への投影。
このとき,
\[
\bf{u}' = \bf{u}\ cos( \theta ) \\
\]
そして \( \theta \) は,
\[
sin( \theta )
= cos( \frac{ \pi }{ 2 } - \theta )
= \frac{ \bf{a} \cdot \bf{u} }{ | \bf{a} |\ | \bf{u} | }
= \frac{ \bf{a} \cdot \bf{u} }{ | \bf{u} | } \\
\]
よって,
\[
{\bf{a}} = ( a_x,\ a_y,\ a_z ) \\
{\bf{u}} = ( u_x,\ u_y,\ u_z ) \\
{\bf{u}}' = ( u'_x,\ u'_y,\ u'_z )
\]
とすると,
\[
\theta = sin^{-1}( \frac{ a_x\ u_x + a_y\ u_y + a_z\ u_z }{ \sqrt{ u_x^2 + u_y^2 + u_z^2 } } ) \\
u'_x = u_x\ cos( \theta ) \\
u'_y = u_y\ cos( \theta ) \\
u'_z = u_z\ cos( \theta ) \\
\]
点 \( P' \) の接平面の法線ベクトル (単位ベクトル) は,
\[
{\bf{p}}' = ( p'_x,\ p'_y,\ p'_z ) = ( \frac{ P'_x }{R},\ \frac{ P'_y }{R},\ \frac{ P' }{R} ) \\
\]
\( \bf{v}' \) が \( \bf{v}_1 \) に投影される角度 \( \theta \) は,
\[
v' = \sqrt{ {v'_x}^2 + {v'_y}^2 + {v'_z}^2 } \\
\ \\
\theta = sin^{-1}( \frac{ p_x\ v'_x + p_y\ v'_y + p_z\ v'_z }{ v' }\ \ ) \\
\quad = sin^{-1}( \frac{ P'_x\ v'_x + P'_y\ v'_y + P'_z\ v'_z }{ R\ v' }\ \ ) \\
\]
そして,
\[
{v_1}_x = v'_x\ cos( \theta ) \\
{v_1}_y = v'_y\ cos( \theta ) \\
{v_1}_z = v'_z\ cos( \theta ) \\
\]
まとめ
移動の \( \Delta t \) 後の速度 \( {\bf{v}}_1 = ( {v_1}_x,\ {v_1}_y,\ {v_1}_z ) \) は,以下のとおり:
\[
v'_x = v_x + a_x\ \Delta t \\
v'_y = v_y + a_y\ \Delta t \\
v'_z = v_z + a_z\ \Delta t \\
\]
\[
v' = \sqrt{ {v'_x}^2 + {v'_y}^2 + {v'_z}^2 } \\
\theta = sin^{-1}( \frac{ P'_x\ v'_x + P'_y\ v'_y + P'_z\ v'_z }{ R\ v' }\ \ ) \\
\]
\[
{v_1}_x = v'_x\ cos( \theta ) \\
{v_1}_y = v'_y\ cos( \theta ) \\
{v_1}_z = v'_z\ cos( \theta ) \\
\]
|
