面上の点 \( P \) にいて,移動の速度が \( {\bf{v}} \) であるとする。 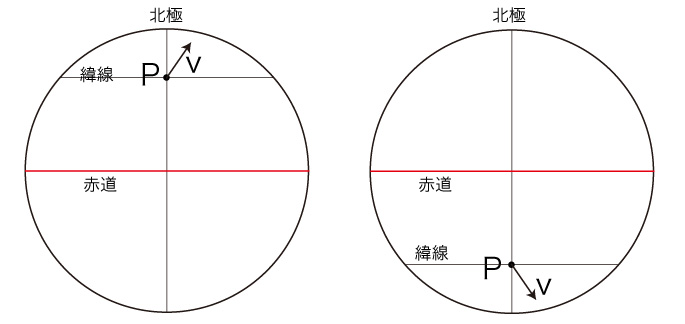
点 \( P \) を通る大円で,これの \( P \) における接線が \( {\bf{v}} \) と同じ向きになるものを,\( S = S( P,\ {\bf{v}} ) \) とする。 \( P \) から \( {\bf{v}} \) の反対方向に \( S \) の上を動いて初めに出会う赤道上の点を,\( Q = Q( P,\ {\bf{v}} ) \) とする。 但し,\( P \) が赤道上の点のときは,\( Q( P,\ {\bf{v}} ) = P \) とする。 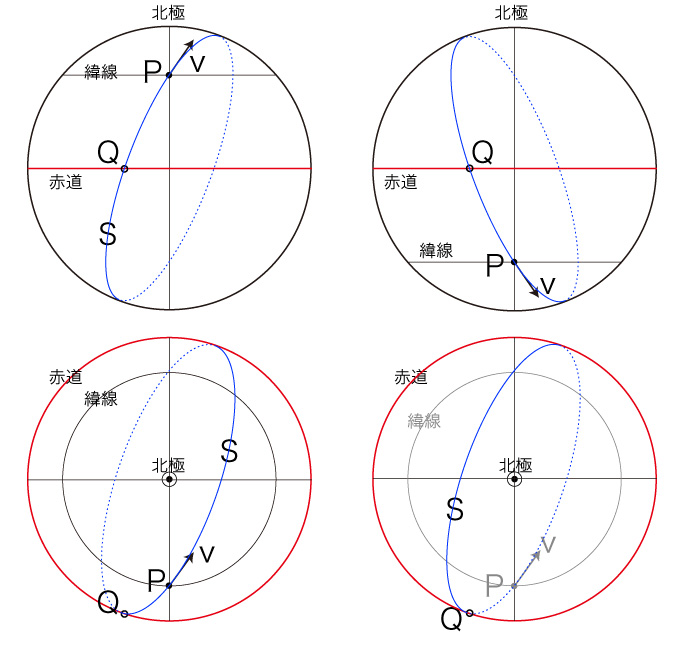 ここで,球体が埋め込まれている空間 (ユークリッド空間) に,球体の中心を原点とするる直交座標を,つぎのように定める。  これを \( ( P,\ {\bf{v}} ) \)-座標と呼ぶ。 また,\( S = S( P,\ {\bf{v}} ) \) を \( ( P,\ {\bf{v}} ) \)-大円,\( Q = Q( P,\ {\bf{v}} ) \) を \( ( P,\ {\bf{v}} ) \)-座標起点と,それぞれ呼ぶことにする。 |