高分子化合物を構成する分子について,つぎのように考える: 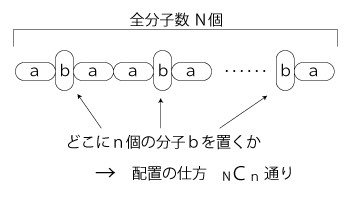
ゴムの「温めると短くなる」は,この「エネルギーが増えると短くなる」に対応していることになる。 いま,この系の「乱雑さ」を,「a型分子とb型分子の数の偏りの無さ」で考える。 偏りは, b型分子が0個のとき,乱雑さは最も小さい。 b型分子が N/2 個のとき,乱雑さが最も大きい。 こうして,乱雑さは,b型分子の個数で表現される。 そこで,「b型分子がn個のとき,乱雑さはn」と定める。 ここでさらに,「乱雑さ」を「熱エネルギー」と言い換える。 どうして「熱エネルギー」のことばなのか? ひとは「熱」を「エネルギー」だと思って,「熱エネルギー」のことばをよく使ってきた。 しかし,「熱」はエネルギーの現象のであって,エネルギーではない。 「熱エネルギー」は,本来,無くてよいことばである。 しかしひとには,「エネルギーは,取り出せないエネルギーであるところの熱になる」の想いがある。 この想いを汲み取ってあげることにする。 そうすると,「熱エネルギー」のことばは,上の形だと,なんとか収まることになるのである。 続けて,系の「状態」を,「乱雑さ」から導かれるものと考える。 即ち,乱雑さがn (「b型分子がn個」) のときの系の状態 W(n) を,
さらに,W(n) の対数
なぜ WではなくSを「エントロピー」と呼ぶことにするかというと,単に Wよりも Sの方が扱い易いからである。 W(n) は一般にひじょうに大きな数になる。 大きな数を扱うときの常套は,「桁数」に言い換えることである。 (対数とは,桁数のことである!) 実際,これで (「乱雑さ」と「状態」の対応であるところの) 熱エネルギーとエントロピーの対応グラフが,以下のように書ける。 スターリングの近似公式を用いて,
= N log N ー n log n ー (Nーn) log (Nーn)
= ー n log n + n log N ー (Nーn) log (Nーn) + (Nーn) log N = (ーn) ( log n ー log N ) ー (Nーn) ( log (Nーn) ー log N ) = ーn log n/N ー (Nーn) log (1ーn/N ) = N ( ーn/N log n/N ー (1ーn/N) log (1ーn/N ) = ーN ( p(n) log p(n) + (1ーp(n)) log (1ーp(n) ) )
こうして,Sのグラフは,
y=x log x + (1ーx) log (1ーx) のグラフは,つぎのようじなる ( 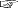 y= (1ーx) log (1ーx) のグラフ): y= (1ーx) log (1ーx) のグラフ):
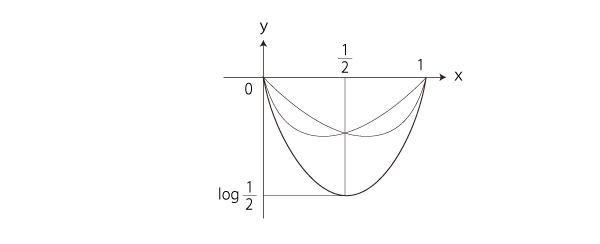
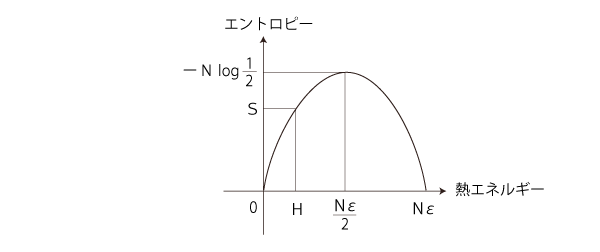
「エントロピー増大則」を満たすのは,つぎの部分: 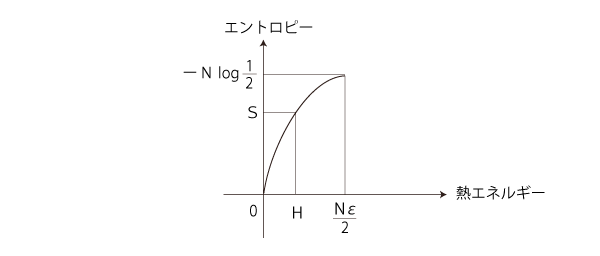
温度β = dS/dH をグラフに記入するならば: 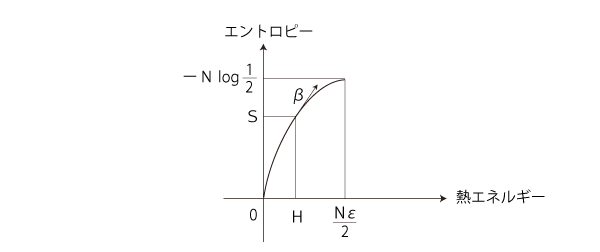
また,このグラフから,温度βと熱エネルギーHの対応グラフも読み取れる:
βの増加と Hの減少が対応 β= ∞ と H = 0 が対応 なお,βとHの対応式は,H = Nε/ (eεβ +1 )
= dS/dp × dp/dH = d(ーN (p log p + (1ーp) log (1ーp) )/dp × d(H/(Nε))/dH = ーN ( ( log p+ p・1/p ) + ( (ー1) log (1ーp) + (1ーp)・(ー1/ (1ーp))) × 1/(Nε) ) = ーN ( log p+ 1 ー log (1ーp) ー1 ) × 1/(Nε) ) = ー log p/(1ーp) /ε ⇐⇒ p/(1ーp) = eーεβ ⇐⇒ p = (1ーp) eーεβ ⇐⇒ p (1+ eーεβ ) = eーεβ ⇐⇒ p = eーεβ / (1+ eーεβ ) = 1 / (eεβ +1 ) ⇐⇒ H = Nε/ (eεβ +1 ) |