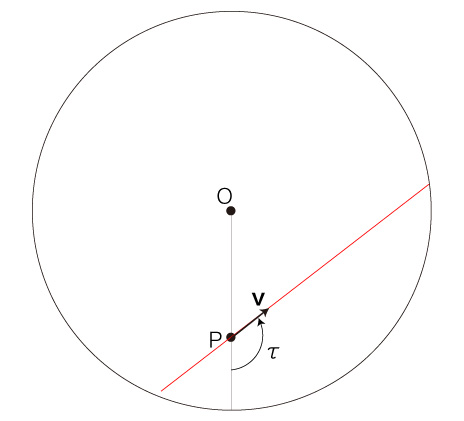
自転する円板状の速さ \( v = | \bf{v} | \) の移動は,\( P \) での速度 \( \bf{v} \) の向きを変えることになる。 この変化が,「加速度」に表現される。 また移動は,位置の変化により,慣性力加速度を被ることになる。 即ち,円板の自転による回転速度が<回転の中心からの距離>によって異なることで,移動は回転速度の変化を慣性力加速度として被ることになる。 これを踏まえたところで,つぎの設定をする: 時間 \( \Delta t \) [時間単位] で,移動がつぎの点 \( P' \) に到ったとする: 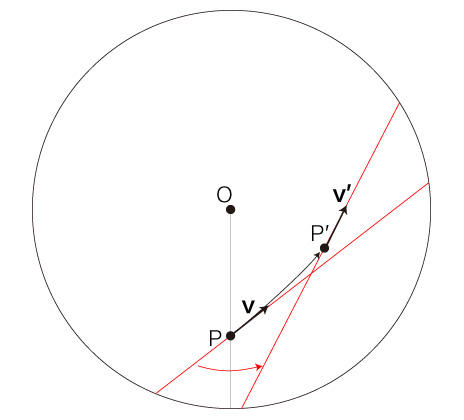
円板の自転による \( P \) における回転速度を \( \bf{w} \),\( P' \) における回転速度を \( \bf{w'} \) とする: 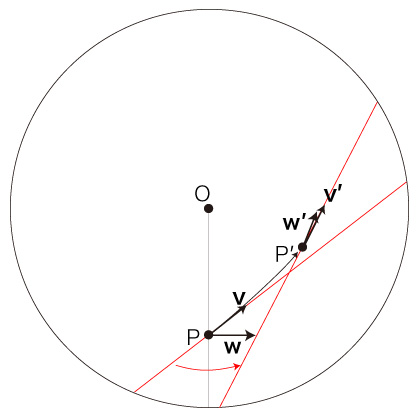
\( P \) における速度と \( P' \) における速度の比較は,自転円板の上に立つ観察者による比較である。 よってこれは, \( {\bf{v}} - {\bf{w}} \) と \( {\bf{v'}} - {\bf{w'}} \) の比較になる。 求めようとしている加速度は,つぎのものである:
\( P \) と \( P' \) の位置関係は,つぎのようになる: 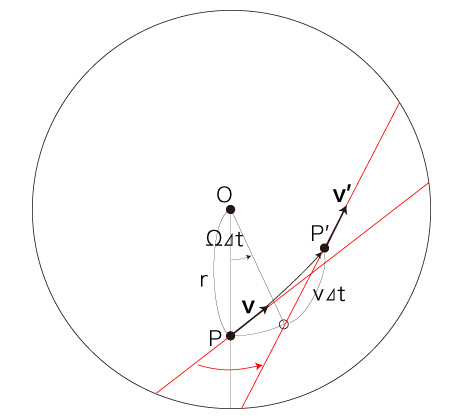
角度 \( \theta,\ a \) をつぎのようにおく: 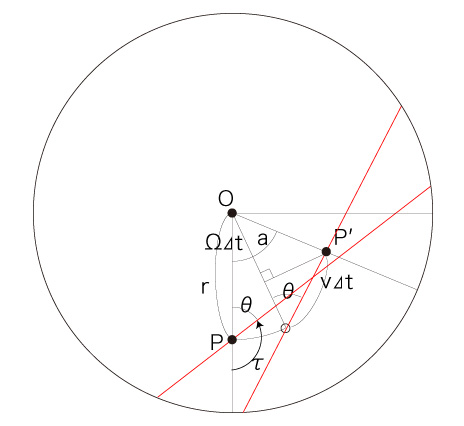
このとき,つぎが成り立つ: 後の計算でこれを用いる。 座標をつぎのようにとる: 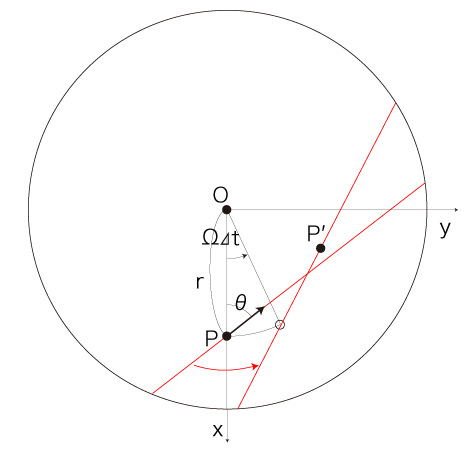
このとき, \[ {\bf{v}} = ( v_x,\ v_y ) \\ {\bf{w}} = ( w_x,\ w_y ) \\ {\bf{v'}} = ( v'_x,\ v'_y ) \\ {\bf{w'}} = ( w'_x,\ w'_y ) \] は: \[ v_x = - v\ cos( \theta ) \\ v_y = v\ sin( \theta ) \\ \ \\ \ \\ w_x = 0 \\ w_y = r\ \Omega \\ \ \\ \ \\ v'_x = - v\ ( cos(\theta) cos(\Omega \Delta t) + sin(\theta) sin(\Omega \Delta t) ) \\ v'_y = v\ ( sin(\theta) cos(\Omega \Delta t) - cos(\theta) sin(\Omega \Delta t) ) \\ \ \\ \ \\ w'_x = - \overline{ OP'}\ \Omega\ ( sin(a)\ cos(\Omega \Delta t) + cos(a)\ sin(\Omega \Delta t) ) \\ w'_y = \overline{ OP'}\ \Omega\ ( cos(a)\ cos(\Omega \Delta t) - sin(a)\ sin(\Omega \Delta t) ) \\ \] \( {\bf v'} - {\bf v} \) は, \[ \frac{ {\bf v'} - {\bf v} }{ \Delta t } \longrightarrow ( - v\ \Omega\ sin(\theta),\ - v\ \Omega\ cos(\theta) ) \ \ \ ( \Delta t \rightarrow 0 ) \] \( {\bf w'} - {\bf w} \) は, \[ \frac{ {\bf w'} - {\bf w} }{ \Delta t } \longrightarrow ( - r \Omega^2 - v \Omega sin(\theta),\ - v \Omega\ cos(\theta) ) \ \ \ ( \Delta t \rightarrow 0 ) \] よって,移動 \( ( P, {\bf{v}} ) \) にかかる加速度は, \[ \begin{align} & \ ( - v \Omega\ sin(\theta),\ - v \Omega\ cos(\theta) ) \\ & \ - ( - r \Omega^2 - v \Omega sin(\theta),\ - v \Omega\ cos(\theta) ) \\ \ \\ = & \ ( r \Omega^2,\ 0 ) \end{align} \] 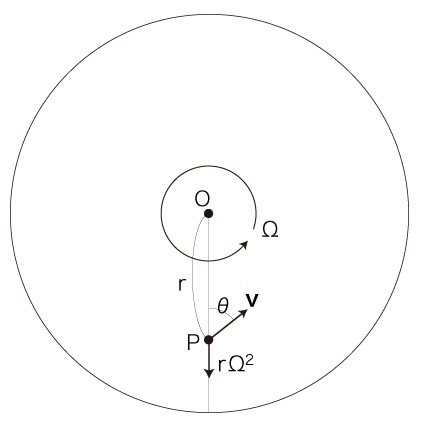
そして, \[ sin( \theta ) = sin( \pi - \tau ) = sin( \tau ) \\ cos( \theta ) = cos( \pi - \tau ) = - cos( \tau ) \] なので,上の式はつぎのようになる: \[ \begin{align} & \ ( - v \Omega\ sin(\tau),\ + v \Omega\ cos(\tau) ) \\ & \ - ( - r \Omega^2 - v \Omega sin(\tau),\ + v \Omega\ cos(\tau) ) \\ \ \\ = & \ ( r \Omega^2,\ 0 ) \end{align} \] |
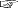 計算
計算