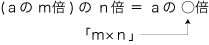
「n÷m」は「mとかけてnになる数」を意味するが,「mとかけてnになる」には m×○=n と ○×m=n の2通りがある。 数が自然数のとき,m×○=n から「n÷m」が立式される算数の問題は,つぎのようなものである:
m×○=n が立式される問題と ○×m=n が立式される問題は,見掛けがかなり (劇的に?) 違ってくる。そこで,前者のタイプの問題に対するわり算の立式が伝統的に「包含除」と呼ばれ,後者の場合が「等分除」と呼ばれてきた。 数が分数のときは,m×○=n から「n÷m」が立式される問題は,つぎのようなものである:
「mグラムの○倍がnグラム」から「m×○=n」が導かれる論理はつぎのようになる:
よって,mグラムの○倍は,グラムのm倍の○倍。 積の定義から,グラムのm倍の○倍はグラムの (m×○) 倍。 この段階になると,「等分除・包含除」という対立のさせ方も無意味になる。 「n÷m」に「包含除・等分除」の2つの意味があるのではない。「n÷m」が立式される問題の構造には, m×○=n で応じるものと ○×m=n で応じるものの2通りがある。ここが要点である。( 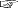 <倍の合成>を構造とする問題の解法) <倍の合成>を構造とする問題の解法)
「等分除・包含除」という擬似論理の用語は,ミス・リーディングである。 |