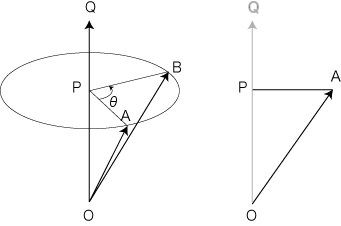
P は,つぎの条件で定まる: 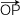 = k = k 
 ・ ・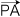 = 0 = 0
そしてこの条件より:
 ・ ・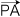 =
=
 ・
( ・
(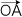 ー ー 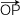 )
= )
=
 ・
( ・
(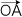 ー k ー k  ) )
=  ・ ・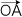 ー k | ー k | |2
= |2
=  ・ ・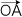 ー k ー k
よって, k =  ・ ・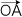 =
qx
ax
+
qy
ay
+
qz
az
=
qx
ax
+
qy
ay
+
qz
az
| 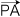 | = r に対し: | = r に対し:
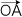 |2
ー | |2
ー |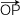 |2
= ax2
+ ay2
+ az2
ー k2 |2
= ax2
+ ay2
+ az2
ー k2
B は,つぎの条件で定まる:  ・ ・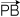 = 0 = 0
| 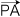 | = | | = |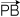 | |
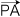 ・ ・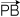 = |
= |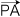 | | | |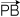 | cos θ
= r2 cos θ | cos θ
= r2 cos θ
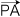 × × 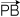 = t
= t  ( t > 0 ) ( t > 0 )
そしてこの条件より:
 ・ ・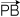 =
=
 ・
( ・
(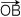 ー ー 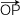 )
= )
=
 ・
( ・
(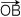 ー k ー k  ) )
=  ・ ・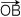 ー k|
ー k| |2
= |2
=  ・ ・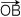 ー k ー k
よって, k = 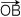 ・ ・ =
qx
bx
+
qy
by
+
qz
bz
=
qx
bx
+
qy
by
+
qz
bz
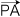 ・ ・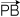 = | = |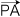 | | | |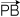 | cos θ = r2 cos θ では, | cos θ = r2 cos θ では,
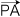 ・ ・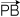 = ( = (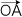 ー ー 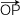 )
・( )
・(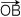 ー ー 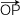 ) )
= ( 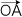 ー k ー k  )
・( )
・(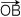 ー k ー k  ) )
= 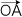 ・ ・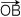 ー k
ー k 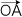 ・ ・ ー k
ー k 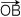 ・ ・ + k2
+ k2  ・ ・
= ax bx + ay by + az bz ー k2 ー k2 + k2 = ax bx + ay by + az bz ー k2 = ax bx + ay by + az bz ー ( ax2 + ay2 + az2 ー r2 ) よって, ax bx + ay by + az bz = ax2 + ay2 + az2 ー r2 + r2 cos θ 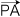 × × 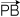 = (
= (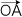 ー ー 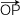 )
× ( )
× (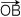 ー ー 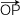 ) )
= ( 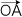 ー k ー k  )
× ( )
× (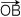 ー k ー k  ) )
= 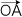 × × 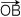 ー k
ー k  × × 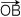 ー k
ー k 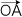 × ×  + k2
+ k2  × × 
= (ay bz ー az by, az bx ー ax bz, ax by ー ay bx) ー k (qy bz ー qz by, qz bx ー qx bz, qx by ー qy bx) ー k (ay qz ー az qy, az qx ー ax qz, ax qy ー ay qx) = (ay bz ー az by ー k qy bz + k qz by ー k ay qz + k az qy, az bx ー ax bz ー k qz bx + k qx bz ー k az qx + k ax qz, ax by ー ay bx ー k qx by + k qy bx ー k ax qy + k ay qx) = ( (ay ー k qy) bz ー (az ー k qz) by ー k ay qz + k az qy, (az ー k qz) bx ー (ax ー k qx) bz ー k qx az + k qz, ax (ax ー k qx) by ー (ay ー k qy) bx ー k qy ax + k qx) ay t = | 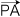 × × 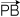 |
= | |
= |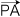 | | | |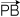 | sin θ
= r2 sin θ | sin θ
= r2 sin θ
よって, 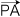 × × 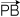 = t
= t  は,つぎのようになる: は,つぎのようになる:
(ay ー k qy) bz ー (az ー k qz) by = k qz ay ー k qy az + r2 qx sin θ (az ー k qz) bx ー (ax ー k qx) bz = k qx az ー k qz ax + r2 qy sin θ (ax ー k qx) by ー (ay ー k qy) bx = k qy ax ー k qx ay + r2 qz sin θ 以上をまとめて:
(2), (4), (5) より,bx が得られる:
ax bx + ay ((ay ー k qy) bx + k qy ax ー k qx ay + r2 qz sin θ) / (ax ー k qx) + az ((az ー k qz) bx ー k qx az + k qz ax ー r2 qy sin θ) / (ax ー k qx) = ax2 + ay2 + az2 ー r2 + r2 cos θ ( ax (ax ー k qx) + ay (ay ー k qy) + az (az ー k qz) ) bx + ay ( k qy ax ー k qx ay + r2 qz sin θ) + az ( ー k qx az + k qz ax ー r2 qy sin θ) = (ax ー k qx) ( ax2 + ay2 + az2 ー r2 + r2 cos θ) ( ax2 ー k qx ax + ay2 ー k qy ay + az2 ー k qz az ) bx = ー ( k qy ax ay ー k qx ay2 + r2 qz ay sin θ ) ー ( ー k qx az2 + k qz az ax ー r2 qy az sin θ ) + ( ax ax2 + ax ay2 + ax az2 ー r2 ax + r2 ax cos θ ) ー k ( qx ax2 + qx ay2 + qx az2 ー r2 qx + r2 qx cos θ ) 左辺 = ( ax2 + ay2 + az2 ー k ( qx ax + qy ay + qz) az ) bx = ( ax2 + ay2 + az2 ー k2 ) bx = r2 bx 右辺 = ー ( k qy ax ay ー k qx ay2 + qz r2 ay sin θ ) ー ( ー k qx az2 + k qz az ax ー r2 qy az sin θ ) + ( ax ax2 + ax ay2 + ax az2 ー r2 ax + r2 ax cos θ ) ー k ( qx ax2 + qx ay2 + qx az2 ー r2 qx + r2 qx cos θ ) = ー k qy ax ay + k qx ay2 ー r2 qz ay sin θ + k qx az2 ー k qz az ax + r2 qy az sin θ + ax ax2 + ax ay2 + ax az2 ー r2 ax + r2 ax cos θ ー k qx ax2 ー k qx ay2 ー k qx az2 + k r2 qx ー k r2 qx cos θ = + ax ax2 + ax ay2 + ax az2 ー k qx ax2 ー k qy ax ay ー k qz az ax ー r2 ax ー r2 qz ay sin θ + r2 qy az sin θ + r2 ax cos θ + k r2 qx ー k r2 qx cos θ + k qx ay2 ー k qx ay2 + k qx az2 ー k qx az2 = ( ax2 + ay2 + az2 ー k ( qx ax + qy ay + qz az ) ) ax ー r2 ax + r2 ( ー qz ay sin θ + qy az sin θ + ax cos θ + k qx ー k qx cos θ ) よって,
同様にして,(2), (3), (5) から by, (2), (3), (4) から bzが,それぞれ得られる:
|