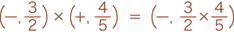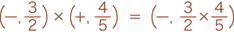正負の数は,<正逆2方向の向きをもつ量>の比を表すものとして,つぎの2つのパートで構成されていました:
- 符号 (向きの変換に関する情報): 同方向なら +,逆方向なら ー。
- 絶対値 (大きさの変換に関する情報): 大きさの比を既知の数で表す。
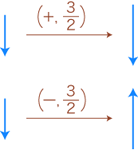
いま正負の数の積を,つぎの場合で考えてみましょう:
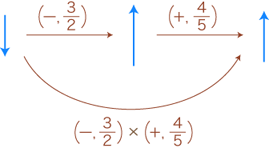
向きの変換に関しては,最初は反転 (−) でつぎは同方向 (+) ですから,あわせて反転 (−) になっています。
大きさの変換に関しては,最初は 3/2 倍でつぎは 4/5 倍ですから,あわせて 3/2 × 4/5 倍になっています。
よって:
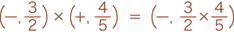
これから類推して,求積の公式がつぎのようになることがわかります:
正負の数 m, nに対し,
1. m ×nの符号は,
・mとnが同符号であるとき +
・mとnが異符号であるとき −
2. |m ×n| = |n| × |m|
|
| 注意 : |
式 |m ×n| = |n| × |m| の左辺の「×」は正負の数の「×」,そして右辺の「×」は正負の数の絶対値の表現に使われている数の「×」です。(両者は別物です!)
──改めて,正負の数の定義を参照してください ( 比の表現 (数表記のきまり):正負の数の場合)。 比の表現 (数表記のきまり):正負の数の場合)。
|
|