1 「一定」 これに,「流れ一定」のものとそうでないものを見る。 「流れ一定」を分析・構造化する。 「時間が 2, 3, ‥‥ 倍になるとき,体積が 2, 3, ‥‥ 倍になる」の表現に到達する。 2 「比例関係」
一方が 2, 3, ‥‥ 倍になるとき,もう一方が 2, 3, ‥‥ 倍になる」 2量に「時間」と「距離」をとれば,運動する物体の「速さ一定」の表現になる。 2量に「体積」と「重さ」をとれば,物の「均質」の表現になる。 そこで,「2量の間の関係で,一方が 2, 3, ‥‥ 倍になるとき,もう一方が 2, 3, ‥‥ 倍になる」は重要な形式だということで,これに名前を与える。 ──「比例関係」である。 3 「一定」(「比例関係」) の個別表現 そこで,これらを区別する表現をつくることにする。 そして,「この時間にこの体積」の表現に到達する。 即ち,つぎのようになる:
対応する時間と体積のペア全体──集合Pとする──は,無限集合になる。 即ち,時間と体積のペア (t, v)がPに属するとき,Pはtのn倍とvのn倍のペア全体になっている。 しかしこのことは,同時に,「Pの要素一つを示すことがP全体を示すことになる」を意味する。 ここに,「5デシリットル/秒」タイプの表現の導入になる。 4 「比例定数」 このとき,時間の単位と体積の単位をそれぞれ一つに固定し (例えば,秒と cm3 ),「この時間にこの体積」の対応から数値と数値の対応を導いてみる。 そして,この数と数の対応に何かきまりが見出されないか,と考える。 このとき,「一定数倍」のきまりに到達する。 即ち,秒の単位に対応する体積が acm3 であるとき,数と数の対応は「a倍」になっている。 定数aを,「比例定数」と呼ぶ。 ここでは,「「一定」(「比例関係」) の個別表現」の授業を示す。 ──────────────────────────────── (授業の主題の提示) T. 始めます。 T. きょう勉強することは,これです。 (板書) いろいろな「流れ一定」がある。 互いに区別できる名前をつくろう。
──────────────────────────────── (既習の押さえ) T. いまみんながどこまで来ているか,確認します。 T. 前々の授業では,いろいろな「流れ一定」を観察しました。 そのいろいろを言い表すのに,「勢いが強い・弱い」「流れが太い・細い」の言い方をしました。。 それから,「流れ一定」って,どんなきまりだろうと考えました。 そして,そのきまりを求めてしまうところまで行っちゃいました。 T. きまりのことばは,けっこう複雑で言いにくかったね。 それで,何回も唱えて身につけるようにしました。 全部で何回唱えたっけ?
T. そして前回の授業では,「比例関係」が出てきました。 これは,「流れ一定」の一般化でした。 T. そして「比例関係」の意味の言い方を,何回も唱えて身につけるようにしました。 全部で何回唱えたっけ?
T. つぎの授業の最初に唱えるぞ,って予告したね。 では,言ってみよう。
T. 「流れ一定」だと,これはどういう言い方になるの?
T. だいじょうぶだね。 これが,今日の勉強に必要なものぜんぶ。 (以上が「導入」と称している部分,以下「展開」と称する本題の部分に入る) ──────────────────────────────── (課題提示) T. (水道の3つの蛇口から水を出して,3つの「流れ一定」をつくる。) ここに,3つの「流れ一定」があります。 それぞれ「流れ一定」ということで,いいね。 本日の課題は,この3つに,互いに区別できる名前をつけようというわけです。 ──────────────────────────────── (課題解決) T. この問題は,実はとっかかりが難しいんだわ。 というわけで,そのとっかかりを先生がつくります。 T. ストップウォッチと,1リットルビーカーを用意しました。 みんなに何をさせようというのでしょう^^
C. たまる量が違ってくる。 T. では,どうぞ。
T. さすが,きちんと記録つけてるね。 時間を変えたりもしているね。 では,報告してもらいましょう。
T. さあ,どうだろう。 名前を考えるとっかかりになった?
C. そうそう T. では,命名してください。
T. あら,できちゃったね。 だけど,時間を変えて測ったりもしたね。 「10秒で1.2デシリットル」の流れは,他にはどんな名前になる?
C. 「20秒で2.4デシリットル」 T. 「10秒で1.2デシリットル」「5秒で0.6デシリットル」「20秒で2.4デシリットル」は,同じ流れを指す名前になってないとまずいぞ。 だいじょうぶ? まずいかだいじょうぶか,考えて。
C. 「10秒で1.2デシリットル」は,「5秒で0.6デシリットル」「20秒で2.4デシリットル」。 C. どれで言っても同じことになる。 T. 「10秒で○デシリットル」だと,測らなくても「5秒で0.6デシリットル」「20秒で2.4デシリットル」になるということ?
C. 「時間が 2, 3, ‥‥ 倍になるとき,体積が 2, 3, ‥‥ 倍になる」 T. じゃあ,実際に測らなくても名前をつくれるということを,やってみますか。 第4の流れとして「3秒で6デシリットル」を考えます。 計算を簡単にするために,数値を簡単にしました。 名前の候補を20個,つくってください。
T. その中で,いちばん使いやすそうな名前といったら,どれになりそう?
T. 実はこれで,本日の授業のゴールに来ちゃいました。 生活では,時間の方を単位にした名前を使うのが,慣習になっています。 このとき「1秒で2デシリットル」は (板書)「2デシリットル/秒」のように書くんだけど,これについてはまた後の授業で。 ──────────────────────────────── (練習) T. 今日は,「第4の流れ」で練習を兼ねたから,特に練習は無し。 ──────────────────────────────── (まとめ) T. では,きょう勉強したことをまとめます。 きょうは,いろいろな「流れ一定」に対して,互いに区別できる名前をつくることをやりました。 名前の形は,「時間に体積を対応させる」でした。 (板書) 「流れ一定」に名前をつける:「時間に体積を対応させる」 ──────────────────────────────── (振り返り) T. 最後に,きょうの授業で,みんながどこからどこまできたか,確かめます。 T. きょうの勉強で必要だったのは,「流れ一定」を「時間が 2, 3, ‥‥ 倍になるとき,体積が 2, 3, ‥‥ 倍になる」に言い表せること。 そして,「流れ一定」に名前をつけるところまできました。 名前のつけ方は,「時間に体積を対応させる」です。 (板書) 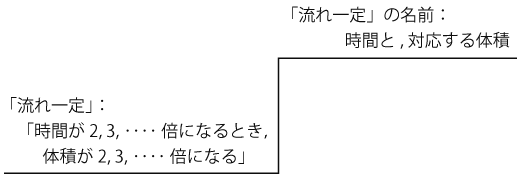
──────────────────────────────── (次時の内容の予告) T. さて,つぎの時間は何をするかですが ‥‥ 「流れ一定」は,比例関係の一つでした。 そこでつぎは,他の比例関係についても,今日やったのと同じことをやってみることにします。 例えば,車の速さに名前をつけるとか,です。 T. それでは,終わります。 |