ペアノの公理は,何を言っているのでしょう? それは, 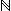 は「系列」である,すなわちつぎの形をしたものである,と言っています: は「系列」である,すなわちつぎの形をしたものである,と言っています:
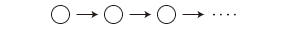
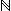 」は,○で示される項の全体です。 」は,○で示される項の全体です。
「1」は,これの先頭の項です。 (条件 1° は,「1」を先頭として定義するものです。──「先頭」を「何の後でもない」ことと条件づけています。) 「f」は,各項にその直後の項 (「後者(successor)」) を対応させる関数です。 (ここでは,記号 → で対応を表現。) ちなみに,1, f(1), f(f(1)), ‥‥ の表記の一つが,「1, 2, 3, ‥‥」です。 以下,ペアノの公理が「系列」の形の過不足無い定義になっていることを,見ていくことにします。 1. 先ず,条件3゜により,1, f(1), f(f(1)), ‥‥ 全体が 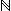 になります。 になります。
特に,  は,fによって全体が一つに連結しています。 は,fによって全体が一つに連結しています。
2. つぎの枝分かれの形は,ありません: 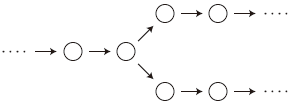
3. つぎの枝分かれの形は,ありません: 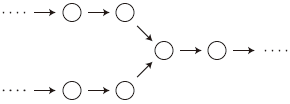
4. 部分ループは,上の2タイプの枝分かれのいずれかを含むので,ありません。 5. つぎの全体ループの形も,ありません: 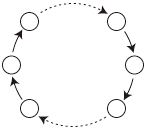
6. つぎの終端の形は,ありません: 
条件1゜より,f(x) は1ではありません。 そして,条件2゜より,f(x) は1以外の項でもありません。 結局,f(x) は存在できません。 7. つぎの無限溯行の形は,ありません: 
8. こうして,つぎの形が残ります: 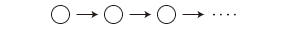
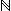 ,1,f)の条件を満たすものになっています。 ,1,f)の条件を満たすものになっています。
|
