「cはaとbの最大公約数」には「a +b +b = c = c 」が対応する(註)。 」が対応する(註)。
そこで,「a +b +b = c = c 」の 」の  を環一般に置き換えて,「cはaとbの最大公約元」を定義する。 を環一般に置き換えて,「cはaとbの最大公約元」を定義する。
| 註 : |
以下が,これの証明。
(*) 一般に,「cはaとbの公約数」と「a +b +b ⊂ c ⊂ c 」は同値 ( 」は同値 (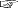 「公約数」が「公約元」)。 「公約数」が「公約元」)。
(1) cがaとbの最大公約数であるとき,a +b +b = c = c : :
(*) より,c ⊂ a ⊂ a +b +b を示せばよい。 を示せばよい。
cがaとbの最大公約数であることから,c=a×m+b×n を満たすm,nが存在する (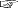 最大公約数)。そしてこれより,c 最大公約数)。そしてこれより,c ⊂ a ⊂ a +b +b 。 。
(2) a +b +b = c = c であるとき,cはaとbの最大公約数: であるとき,cはaとbの最大公約数:
(*) より,aとbの任意の公約数dが ≦c であることを示せばよい。
a +b +b ⊂ d ⊂ d 。よって,c 。よって,c ⊂ d ⊂ d 。これは,dがcの約数であることを示す ( 。これは,dがcの約数であることを示す (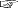 「公約数」が「公約元」の註)。特に,d≦c。 「公約数」が「公約元」の註)。特に,d≦c。
|
|
 +b
+b = c
= c 」が対応する(註)。
」が対応する(註)。
 +b
+b = c
= c 」の
」の  を環一般に置き換えて,「cはaとbの最大公約元」を定義する。
を環一般に置き換えて,「cはaとbの最大公約元」を定義する。
 +b
+b = c
= c 」が対応する(註)。
」が対応する(註)。
 +b
+b = c
= c 」の
」の  を環一般に置き換えて,「cはaとbの最大公約元」を定義する。
を環一般に置き換えて,「cはaとbの最大公約元」を定義する。